만난 적 없어도 서로를 믿게 해주는 디피 헬만 키 교환 알고리즘의 마법

안녕하세요!

오늘은 암호학 분야에서 제가 가장 좋아하는 알고리즘인 디피 헬만 키 교환 알고리즘에 대해 설명드리고자 합니다.

인터넷 상에서 여러 사용자 들은 서로를 어떻게 신뢰할 수 있을까요?

내가 인터넷 상에서 전송하는 정보를 다른 사람이 쉽게 들여다 볼 수 있다면, 아무도 인터넷을 사용하지 않겠죠.

따라서 인터넷 상의 데이터는 암호화 되어 전달되는데요, 이때 암호화 방법으로 대칭키, 공개키 방법 등이 있습니다.

디피 헬만 키 교환 알고리즘은 서로 만난적도, 본 적도 없는 두 사람이 서로를 믿을 수 있는 동일한 암호화 키 를 가지게 해주는 알고리즘입니다.

디피 헬만 알고리즘을 사용하면 지구 반대편의 사람과 내가 단 둘 만 아는 암호화 키를 생성할 수 있습니다. 만나지 않아도, 서로 암호화 키를 직접 교환하지 않아도요!

마치 중고나라 거래에서 본 적 없는 두 사람이 서로를 믿고 물건을 보낼 수 있는 마법같은 상황이죠.

오늘은 보안성을 추구하는 대표적인 메신저인 텔레그램 에도 적용되어 있는 디피 헬만 키 교환 알고리즘의 원리부터 구체적인 동작 방식에 대해 알아보도록 하겠습니다!

암호화의 기본 개념: 대칭키, 공개키 암호화

암호화 방법은 크게 2가지 로 분류 됩니다. 대칭 키 와 공개 키 암호화 방식 이죠. 간단하게 두 방식의 개념을 알아보겠습니다.


암호화, 복호화에 같은 키 를 사용하는 대칭 키 암호화 방법

대칭 키 암호화 방법은 암호화, 복호화에 같은 키 를 사용합니다.

자물쇠를 잠그고 풀 때 같은 키를 사용하는 것 과 마찬가지죠! 직관적으로 쉽게 이해할 수 있습니다.

다만, 자물쇠를 잠구고 풀 때 같은 키를 사용하기 때문에 키를 도난당한다면 누구나 자물쇠를 풀 수 있겠죠?

그래서 키를 하나 더 만든 방법이 공개 키 암호화 방식 입니다.


암호화에는 누구에게나 공개되어 있는 공개 키를, 복호화 에는 수신자 만 아는 비밀 키를 사용하는 공개 키 암호화 방법

자물쇠를 잠그고 풀 때 같은 키 를 사용했던 대칭 키 알고리즘과 달리, 공개 키 암호화 방식에서는 자물쇠를 잠글 때 는 누구에게나 공캐되어 있는 공개 키를, 자물쇠를 풀 때 에는 자물쇠의 주인 만 이 가지고 있는 비밀키 를 사용합니다.

따라서 대칭 키 알고리즘 과 달리 공개 키를 누구에게나 공개해도 상관 없으며 비밀 키 만 잘 관리하면 되므로, 조금 더 키 관리가 수월해 집니다.

대칭 키 알고리즘 에선 자물쇠를 잠그고 풀 때 같은 키를 사용하기 때문에, 자물쇠를 잠그는 사람인 메시지 전송 자 와 자물쇠를 푸는 사람인 메시지 수신 자 2명 모두 키 관리에 주의를 해야 합니다.

하지만, 공개 키 알고리즘 에서는 누구에게나 공개되어 있는 공개 키 로 자물쇠를 잠그고, 자물쇠의 주인이 가지고 있는 비밀키 만으로 자물쇠를 풀 수 있으니 비밀 키 1개 만 잘 관리하면 됩니다.

이때 비밀키 는 자물쇠의 주인 만이 가지고 있고 절대 잃어버려선 안되겠죠!

이러한 대칭 키 암호화 방식의 대표적인 예는 DES, AES 알고리즘이 있으며 공개 키 암호화 방식에는 RSA 알고리즘이 있습니다.

일반적으로 대칭 키 알고리즘은 암호화, 복호화에 2개의 키를 사용하는 공개 키 알고리즘과 달리 하나의 대칭 키를 사용하기 때문에 계산 속도가 더 빠르다는 장점이 있어 현대에서도 공개키와 대칭키 암호화 알고리즘이 그 목적에 따라 같이 쓰이기도 합니다.

https:// 로 시작하는 URL 의 웹 사이트를 접속 할 때, 웹사이트 인증에는 공개 키 암호화 알고리즘을, 데이터 송수신 에서의 암호화 에는 속도가 더 빠른 대칭 키 암호화 알고리즘이 사용됩니다.

이 글 에서는 구체적인 암호화 알고리즘 이 아닌, 대칭 키 자체를 안전하게 생성할 수 있는 방법인 디피 헬만 키 교환 알고리즘에 대해 알아보고자 합니다.

쉽게 이해하는 대칭 키 암호화 알고리즘의 동작 방식


대칭 키 암호화 방법의 구체적인 동작 예시

대칭 키를 생성하는 디피 헬만 키 교환 알고리즘을 바로 살펴보기에 앞서, 대칭 키 암호화가 어떤 식으로 동작하는지 간단하게 알아보겠습니다.

위의 그림은 대칭 키를 각 자리 수 마다 +1 로 정한 후 이를 통해 암호화, 복호화 하는 과정을 보여줍니다.

123 을 전송하려고 할 때, 우리가 정한 각 자리 수 마다 +1 대칭 키를 통해 암호화를 하면 234 가 나옵니다.

암호화 한 234 를 수신 한 수신자 측 에서는, 각 자리 수 마다 -1 대칭 키 를 사용하여 복호화 를 하면 원래의 메시지 인 123 을 얻을 수 있습니다.

너무나 간단하게 보이지만, 대칭 키 알고리즘의 가장 근본적인 원리는 이 개념과 다를 바 없습니다.

DES 나 AES 대칭 키 암호화 알고리즘은 대칭 키 를 조금 더 복잡하고 계산해내기 어렵게 만든 것 뿐이죠.

이러한 대칭 키 암호화 방식은 같은 키 로 암호화, 복호화 하기 떄문에 키를 2개 사용하는 공개 키 암호화 알고리즘에 비해 간단하고 암호화, 복호화 계산 속도가 빠르다는 장점이 있습니다.

하지만 큰 단점이 있는데요, 바로 대칭 키를 도난 당하면 보안이 완전 무너진다는 것 입니다.

대칭 키를 지켜라!


대칭 키가 도난 당하면, 누구나 대칭 키를 통해 복호화가 가능

위의 그림 처럼 대칭 키가 도난당하거나 유출 된 다면, 그 대칭 키로 누구나 암호화 된 메시지를 복호화 할 수 있습니다.

자물쇠 를 잠그고 풀 때 같은 열쇠를 사용하니, 열쇠만 있다면 누구나 자물쇠를 풀 수 있는 것 이죠!

가뜩이나 대칭 키 알고리즘은 자물쇠를 푸는 사람 (메시지 수신자) 말고도 자물쇠를 잠그는 사람 (메시지 전송자) 도 키를 가지고 있어야 하는데 전송자가 여러명이 되면 그만큼 키를 분실하거나 도난당할 확률도 늘어납니다.

이를 해결할 수 있는 방법은 없을까요?


대칭 키를 쪼개서 반반 가지고 있으면 어떨까?

대칭 키 를 분실해도 안전한 방법은 없을까요?

가장 간단한 방법으로는, 자물쇠를 잠그는 사람과 푸는 사람에게 대칭 키 를 쪼개서 반반 가지고 있는 방법을 떠올릴 수 있습니다.

서로 온전한 대칭 키 를 가지고 있는 것이 아닌 반 쪽 키 만 가지고 있고, 서로의 반쪽 키를 합쳐서 대칭키를 만드는 것 이죠.

이때 중요한 점은, 중간에 다른 사람이 반 쪽 키 두개를 모두 탈취 한다고 해도 온전한 대칭 키를 만들 수 없어야 합니다.

그래야 대칭 키 알고리즘이 키를 도난당해도 안전하다는 것 을 보장할 수 있죠.

또한, 반쪽 키를 합쳐서 온전한 키를 만드는 방법은 공개되어 있어야 합니다.

그래야 누구나 대칭 키 알고리즘을 사용할 수 있으니까요.

메시지 송신자와 수신자 둘 만 대칭키 를 만드는 방법을 안다면 애초에 대칭 키를 만드는 방법을 서로 공유해야 하는데 이 과정에서 키를 만드는 방법 자체가 도난 당하는거나 대칭 키를 도난당하는거나 마찬가지죠.

또한 둘 만 아는 대칭 키를 만드는 방법을 사용한다면, 사용자가 늘어 날 수록 대칭 키를 만드는 방법도 사용자 수에 따라서 늘어나야 하며 오히려 대칭 키를 만드는 방법이 유출되지 않게 관리를 해야하는 상황이 옵니다.

정리해보면, 우리가 원하는 이상적인 대칭 키 알고리즘은 다음과 같습니다.

중간에 다른 사람이 반 쪽 키 두개를 모두 탈취 한다고 해도 온전한 대칭 키를 만들 수 없다.
반쪽 키를 합쳐서 온전한 키를 만드는 방법은 공개되어 있어야 한다.

이 두가지 요구 사항이 과연 동시에 만족될 수 있을까요?

딱 봐도 서로 모순되지 않나요?

하지만, 마법같은 디피 헬만 키 교환 알고리즘은 이 어려운 걸 간단한 수학을 이용해 해냅니다.

디피 헬만 키 교환 알고리즘의 마법

마법같은 디피 헬만 키 교환 알고리즘을 살펴보기에 앞서, 정말 정말 간단한 수학적 개념 딱 1개만 보고 가겠습니다.

바로 양방향 함수와 일방향 함수 입니다.

양방향 함수: 거꾸로 계산하기도 쉬워요


양방향 함수 예시

위의 그림은 양방향 함수인 Y = 2X 의 예시 입니다.

Y = 2X 는 위의 그림 처럼 X 가 주어졌을때 Y를 구하기도 쉽고, Y 가 주어졌을 때 역으로 X 를 구하기 도 쉽습니다.

이처럼 입력값이 주어졌을때 결과값을 구하기 쉽고, 역으로 결과값이 주어졌을때 입력값 도 구하기 쉬운 함수를 양방향 함수라고 합니다.

일방향 함수: 거꾸로 계산하기는 어려워요


일방향 함수 예시

위의 그림은 일방향 함수인 Y = a^x mod b 의 예시 입니다.

Y = a^x mod b 는 위의 그림 처럼 a, b 는 알고 있고 x 가 주어졌을때 y를 구하기는 쉽지만, y 가 주어져 있을 때 역으로 x 를 구하기는 어렵습니다.

위의 그림 처럼 a = 3, b = 5, y = 4 일 때 4 = 3^x mod 5 를 만족하는 x 를 구하는 방법은 x 를 1 부터 하나하나 대입해보는 수 밖에 없죠.

정말 사실일까요?

이러한 문제는 이산 대수 문제 라고 불리며 아직까지 이를 효율적으로 계산하는 방법은 수학적으로 알려져 있지 않습니다.

하나하나 대입해 보거나, 아무리 효율적인 알고리즘을 사용해도 지수적 시간 복잡도를 가집니다.

그럼 한쪽 방향으로만 계산하기 쉬운 일방향 함수를 어디다 쓸까요?

바로 반쪽 짜리 키로 대칭 키를 만드는데 사용할 수 있습니다.

디피 헬만 키 교환 알고리즘의 구체적인 동작 원리


디피 헬만 키 교환 알고리즘의 동작 원리

앞서 살펴봤던, 한쪽 방향으로만 계산하기 쉬운 일방향 함수의 특징을 디피 헬만 키 교환 알고리즘 에서는 송수신자 둘 만 생성 가능한 대칭 키를 만드는데 사용합니다.

위의 그림 처럼, g 와 p 는 공개되어있는 상태에서 데이터 송수신자는 자신만 아는 반쪽짜리 키 인 a, b 를 가지고 있습니다.

그 후, 서로의 반쪽짜리 키로 g^a mod p 와 g^b mod p 를 만들어 서로에게 보냅니다.

서로가 교환한 g^a mod p, g^b mod p 와 자기만 알고있는 반쪽 짜리 키 인 a, b 로 (g^a)^b mod p = (g^b)^a mod p = g^ab mod p 를 만들 수 있습니다.

서로의 반쪽 짜리 키 a, b 를 통해 g^ab mod p 라는 서로 같은 대칭 키를 만들어 냈죠!

그렇다면 g^ab mod p 는 안전할 까요?


디피 헬만 키 교환 알고리즘의 안전성

송수신자는 서로 반쪽짜리 키 인 a, b 를 직접 교환한 것 이 아닌 g^a mod p 와 g^b mod p 를 교환했습니다.

따라서 중간에 다른 사람이 g^a mod p 와 g^b mod p 를 탈취해도, 이를 통해 서로를 곱한 g^(a+b) mod p 까지 만 얻을 수 있습니다.

우리의 대칭키인 g^ab mod p 는 결코 만들지 못하죠!

이는 앞서 살펴본 이산 대수 문제로 설명이 가능합니다.

이산 대수 문제는 y = g^x mod p 에서 g, p, x 가 알려져 있을때 y 를 계산하는 건 쉽지만, g, p, y 가 알려져 있을 때 역으로 x 를 구하는 방법은 어렵다 였는데요.

따라서 다른 사람이 g^a mod p 와 g^b mod p 를 탈취해도, 이를 통해 반쪽 짜리 키 인 a, b 를 알아내기 어렵기 때문에 a, b 를 가지고 있는 데이터 송수신 자가 a, b 로 만든 대칭 키인 g^ab mod p 는 만들지 못하며, 아무리 노력해봐야 g^a mod p 와 g^b mod p 로 서로를 곱한 g^(a+b) mod p 까지 만 만들수 있다 가 증명됩니다.

결국, 대칭 키 인 g^ab mod p 를 만드려면 반쪽 짜리 키 원본인 a, b 를 알아야 하죠!

이처럼 디피 헬만 키 교환 알고리즘은 이산 대수 문제라는 일방향 함수의 특징을 그대로 활용하여 만난 적도, 본 적도 없는 두 사람 만이 아는 비밀의 대칭 키를 만들어 내는 마법같은 알고리즘 입니다.

또한 정보가 중간에 탈취되도, 우리의 대칭키는 이산 대수 문제로 인해 탈취한 정보 만으로 만들기 어렵다는 것이 보장됩니다!

정말 대단하지 않나요?

중간에서 키를 아예 바꿔버리는 Man-in-the-middle 공격


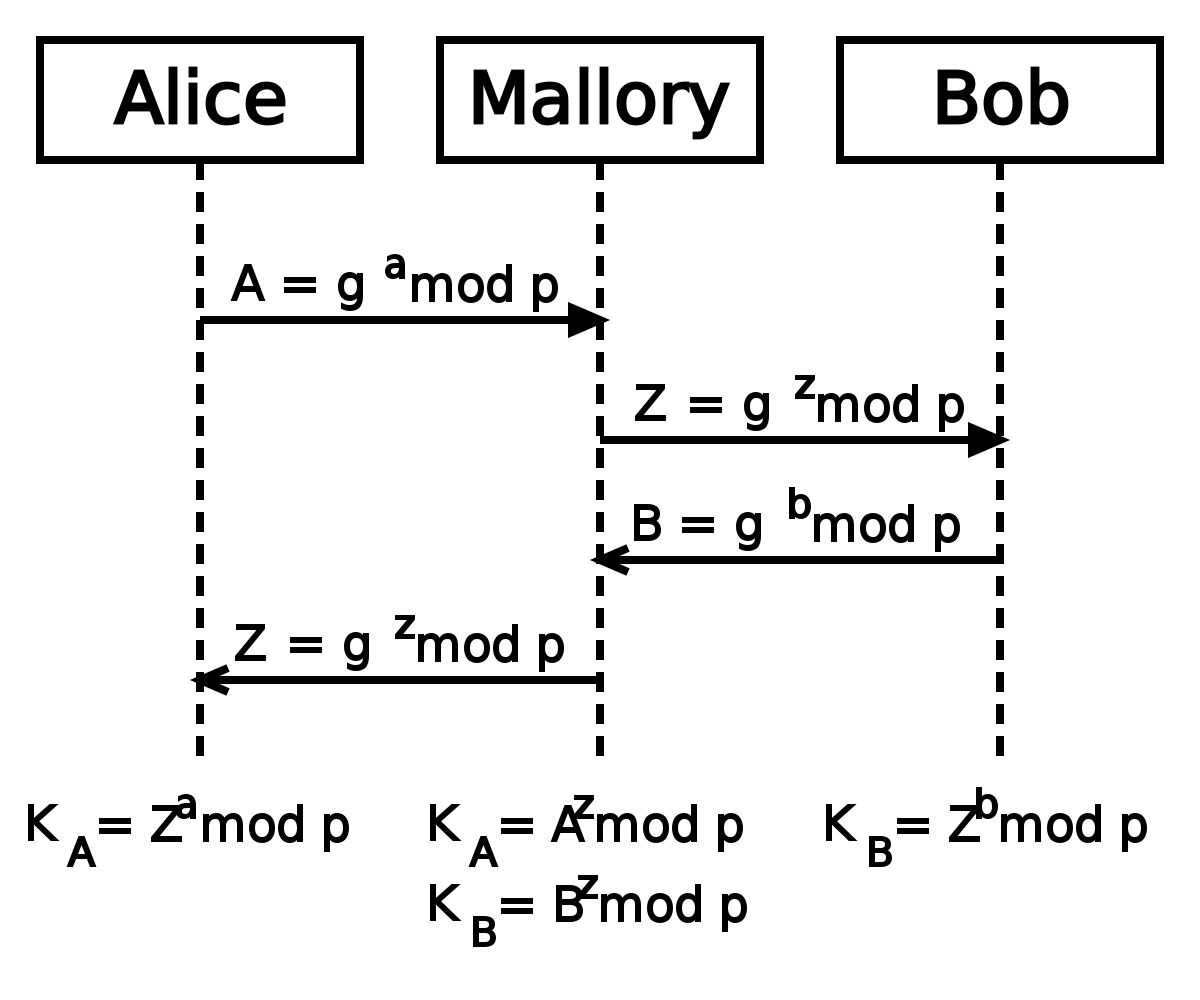Man In The Middle (중간자) 공격 예시

하지만 이러한 이산 대수 문제를 기반으로 하는 디피 헬만 키 교환 방식도 완벽한 건 아닙니다.

중간에 정보를 탈취하는 해커가 정보 탈취 뿐 만 아니라 송수신 자 에게 또다른 데이터를 전송할 수 있는 경우에는 Man In The Middle (중간자) 공격이 가능합니다.

예를들어, g^a mod p 를 탈취한 후g^t mod p 처럼 아예 자신의 반쪽짜리 키 인 t 로 만든 키를 원래의 키로 속여버리는 것 이죠!

양쪽의 키 를 모두 속여서 전송할 수 있다면 위의 사진 처럼 데이터 송수신 자 사이에서 자신의 키로 한번 더 암호화, 복호화 하여 데이터 송수신이 정상적으로 이루어지는 것 처럼 포장할 수 있습니다.

텔레그램 메신저 에 적용된 디피 헬만 키 교환 알고리즘


디피 헬만 키 교환 알고리즘이 적용되어 있는 텔레그램 메신저

이러한 디피 헬만 키 교환 알고리즘은 보안성을 앞세우는 텔레그램 메신저에 적용되어 있습니다.

텔레그램 FAQ 웹 페이지 에서 그 사실을 확인할 수 있습니다.

Q: What is this ‘Encryption Key’ thing?

When a secret chat is created, the participating devices exchange encryption keys using the so-called Diffie-Hellman key exchange. After the secure end-to-end connection has been established, we generate a picture that visualizes the encryption key for your chat. You can then compare this image with the one your friend has — if the two images are the same, you can be sure that the secret chat is secure, and no man-in-the-middle attack can succeed.

텔레그램 FAQ 웹 페이지 에서는 위처럼 자신들의 암호화 키 에 디피헬만 키 교환 알고리즘이 적용되어 있다고 명시하고 있습니다.

또한 중간자 공격을 막기 위한 아이디어로 데이터 송수신 자가 생성한 대칭키가 서로 동일한 지 확인하는 방법을 사용하고 있습니다.

이는 중간자 공격으로 인해 대칭 키가 중간에 변경되었다면, 송수신자 측 에서 각각 생성한 대칭키가 서로 달라지기 때문이 이를 비교하여 중간자 공격이 발생하였는지 를 확인할 수 있기 때문입니다.

보안성을 내세우는 텔레그램에도 적용되어 있는 디피 헬만 키 교환 알고리즘의 원리, 이제 이해하셨나요?

결론: 마법같은 수학과 알고리즘

대칭키, 공개키 암호화 방법과 디피 헬만 키 교환 알고리즘의 원리 부터 동작 방식, 텔레그램 의 적용 예시 까지를 이 글에서 알아보았습니다.

저는 디피 헬만 키 교환 알고리즘을 학부 수업 중 ‘암호학과 보안’ 수업에서 처음 배웠는데요, 처음 설명을 들었을때 에는 정말 마법같다는 생각이 들었습니다.

디피 헬만 키 교환 알고리즘의 간단한 아이디어, 그 뒤엔 정교한 수학 개념이 자리잡고 있었으며 이러한 수학적인 개념이 실제 세계에 적용되는 것 자체가 너무나도 매력적 이라고 느꼈습니다.

아마도 이러한 이유가 프로그래머가 수학을 조금씩 이라도 배워야 하는 이유가 아닐까요?

현실의 문제를 해결하는 방법 중 하나가 수학 이니까요!

항상 읽어주셔서 감사합니다.